Daily Science Quote #20

The making of nontrivial theory for ecology is best done by field naturalists provided that these know what science is all about.

Robert MacArthur, 1962

Daily Science Quote #19

This is another way of saying that objects such as these cannot be explained as coming into existence by chance. As we have seen, to invoke chance, on its own, as an explanation, is equivalent to vaulting from the bottom to the top of Mount Improbable's steepest cliff in one bound. And what corresponds to inching up the kindly, grassy slopes on the other side of the mountain? It is the slow, cumulative, one-step-at-a-time, non-random survival of random variants that Darwin called natural selection. The metaphor of Mount Improbable dramatizes the mistake of the sceptics quoted at the beginning of this chapter. Where they went wrong was to keep their eyes fixed on the vertical precipice and its dramatic height. They assumed that the sheer cliff was the only way up to the summit on which are perched eyes and protein molecules and other supremely improbable arrangements of parts. It was Darwin's great achievement to discover the gentle gradients winding up the other side of the mountain.

Richard Dawkins, in Climbing Mount Improbable.

Daily Science Quote #18

Ecology often seems dominated by theoretical bandwagons driven by charismatic mathematicians, lost to the realization that good ecology rests on a foundation of natural history and progresses by use of proper scientific methods.

Paul K. Dayton, 1980

Jack Layton, Brian Alters and The State of Science in Our Society

This thursday I had the pleasure of participating in a meet and greet with the leader of the NDP, Jack Layton, at Publix Bar on St-Laurent. Being a member of the NDP and all, I thought it would be a good opportunity to pick Jack's brain about the abyssmal state of science education in the country. In order to do so, I decided to invoke the case of Professor Brian Alters,a McGill professor who had a research grant turned downed by the SSHRC (Social Science and Humanities Research Council). Professor Alters was interested in investigating the adverse effects that Intelligent Design was having on the theory of evolution and therefore science education in Canada. Amazingly, the SSHRC ruled that Alters had not supplied "adequate justification for the assumption in the proposal that the theory of evolution, and not intelligent design theory, was correct"(The Gazette, April 5 2006). Of course, this rejection of his research proposal was a first-hand demonstartion of the phenomenon Professor Alters wanted to investigate.

In any event, I told Jack about this and he said he never heard about this case and that I should email him all the facts, which I will be doing in a relatively short time. Nevertheless, I think that the Alters case is symptomatic of the poverty of science education in Canada. A surprising amount of people believe that the theory of evolution is invalid or that it has somehow been disproven. For example, my next door neighbour, who has a Phd in Biophysics, thought that the theory of evolution was rejected sometime in the 1980s! It just boggles the mind that people who are very intelligent can get so badly misinformed about certain issues.

Daily Science Quote #17

Nature first, then theory. Or, better, Nature and theory closely intertwined while you throw all your intellectual capital at the subject. Love the organisms for themselves first, then strain for general explanations, and, with good fortune, discoveries will follow. If they don't, the love and the pleasure will have been enough.

-E. O. Wilson, Naturalist

Daily Science Quote #16

I am myself an empyric in natural philosophy, suffering my faith to go no further than my facts. I am pleased, however, to see the efforts of hypothetical speculation, because by the collisions of different hypotheses, truth may be elicied, and science advanced in the end.

Thomas Jefferson

Daily Science Quote #15

Objectivity cannot be equated with mental blankness; rather, objectivity resides in recognizing your preferences and then subjecting them to especially harsh scrutiny—and also in a willingness to revise or abandon your theories when the tests fail (as they usually do).

Stephen Jay Gould, Natural History 107 (December 1998): 18.

The Idiocy of Rex Murphy

On the May 16th airing of The National, Rex Murphy decided to make a complete fool of himself by making his usual pseudo-intellectual attempt at serious commentary on important issues. The important issues at hand were the gun registry and the Kyoto Protocol. While his opinions on the gun registry were misguided, they were not completely dishonest. However, he committed massive intellectual dishonesty with the following statement:

Now, Kyoto is not a registry, but it has the same impulse at its centre, vagueness of intention surrounding an amorphous good cause. The science is contentious, regardless of what the propagandists of global warning will tell you. It is advocacy-driven and as much a lobby as General Motors. (Author's emphasis)

Contentious, you say? My, aren't we scientifically illiterate? Maybe poor old Rex worked himself into a stupor by reading the trash that Bjorn Lomborg has been publishing recently or whatever tripe is being forwarded by such respectable journals as Oil & Gas Monthly (nothing like corporate mouthpieces to get the straight goods, eh?). Of course, if good old Mr. Murphy could be bothered to properly inform himself by talking to actual scientists or reading the scientific literature on the subject, perhaps he would discover that the science is not at all contentious. Global warming is a fact. According to the IPCC (Intergovernmental Panel on Climate Change), temperatures have already risen 0.4 to 0.8 degrees Centigrade in the last century or so. In addition, the best models on climate have demonstrated that natural causes of global warming are insufficient in causing the increases, but natural causes along with anthropogenic causes would be able to. In fact, the recent increases in temperature are modelled quite well by just taking into account anthropogenic causes, indicating that natural sources of global warming are minimally contributing to the recent spike in temperatures. If current trends continue as they most likely will, then one can expect surface temperatures to rise 1.2 to 3.5 degrees in the next century, causing massive climate change.

Ah well, maybe next week Rexy boy will declare that the science behind evolution and the theory of relativity are "contentious".

Daily Science Quote #14

The worst thing that can happen during the 1980s is not energy depletion, economic collapse, limited nuclear war, or conquest by a totalitarian government. As terrible as these catastrophes would be for us, they can be repaired within a few generations. The one process ongoing in the 1980s that will take millions of years to correct is the loss of genetic and species diversity by the destruction of natural habitats. This is the folly that our descendents are least likely to forgive us.

E.O. Wilson, Gaia Atlas of Planet Management, 1993, p 159.

Daily Science Quote #13

Like most mathematicians, he [Alfred Lotka] takes the hopeful biologist to the edge of the pond, points out that a
good swim will help his work, and then pushes him in and leaves him to drown.

Charles Sutherland Elton, in the Journal of Animal Ecology, vol.4, p.148-149, 1935

Daily Science Quote #12

Nothing in science -- nothing in life, for that matter -- makes sense without theory. It is our nature to put all knowledge into context in order to tell a story, and to re-create the world by this means.

E.O. Wilson

Daily Science Quote #11

Nothing in science -- nothing in life, for that matter -- makes sense without theory. It is our nature to put all knowledge into context in order to tell a story, and to re-create the world by this means.

E.O. Wilson

The Paradox of Enrichment: The Theory

WARNING: This post contains calculus, phase planes, time series and other mathematical concepts that may be horrifically boring to the non-mathematically inclined. Reader discretion is advised.

A Short Aside: Exponential and Logistic Growth

Before I get into the hot and heavy mathematics and theory behind the paradox of enrichment, I thought it would be a good idea to introduce two fundamental equations of ecology: the exponential and logistic growth curves. While many people have heard of exponential growth as it is used in many fields, logistic growth is usually restricted to ecology.

Exponential growth is normally formulated and derived in the following way:
the rate of growth of a population N, dN/dt, is proportional to that population. In order to make proportionality explicit, we introduce a proportionality constant, r. Therefore, we have the following equation:

dN/dt= rN

While this is all nice and dandy, what us crazy ecologists normally want to know is what will the population size be at any instant of time, if we know the starting population size and the rate of growth. To do that, we are going to have to do some intergration (yay, calculus). First, let us rearrange the equation:

dN/N = rdt, then lets do the intergration and the algebra:


And now we have a general equation for exponential growth. However, if things in nature grew exponentially, then the world would be covered in an immense blob of bacteria. Therefore, there must be some sort of regulation or limitation (important distinction here, regulation means density-dependent effects, such as predation, disease, food, while limitation means density-independent factors, such as temperature, water salinity and other such factors) acting on the population. Let us assume that density-dependent factors are regulating population size. Therefore, in a certain environment, our organism of interest has a limit to its maximum sustainable population size. We shall call this population size the carrying capacity of the environment for the organism of interest. We shall symbolize the carrying capacity by the parameter K in our model. Therefore, adding K into our previous equation for exponential growth, we obtain the following:

dN/dt = rN (1- N/K)


As we can see, when the population reaches the size of K (when N=K), the rate of growth is 0. Also, if the population started at a size greater than K (No > K), there would be a negative growth rate till the population reached the carrying capacity. Here are two graphical examples, showing the differences between exponential and logistic growth when the initial value of N is 5, r is 1 and K is 10:


Now, let us derive a general solution for this differential equation. It is a bit more tricky than the solution for exponential growth, so try to follow along:








(Note: At one point, I used partial fraction in order to simplify the integral. Solving partial fractions are relatively easy. In the above example, we had 1= A(1-x) + Bx after we multiplied both sides by x(1-x). We then look at the case when x=0, so
1=A(1-0) + B*0 -> 1=A. Next, we look at the situation where x is not equal to zero, so 1= A - Ax + Bx. Since we know that A=1, then 0= Bx - Ax -> B=A=1.)

And now we have a solution for logistic growth. Wasn't that fun? Wow, my short asides are gigantic... I guess I'll never get published in Nature with such a verbose writing style, but that's their lost. Anyways, back to the topic at hand.

Lokta-Volterra Equations for Predator-Prey Dynamics

In the aside, we discussed the case of the population dynamics of a single species. What would happen if we had two species interacting, say a prey and a predator species? The simplest way of formulation such a situation mathematically is the Lokta-Volterra Equations:



Where N is the prey population, P is the predator population, r is the prey's growth rate, a represents the uptake of the predator of the prey, e is the efficiency of the predator in turning prey biomass into predator biomass and m represents the mortality rate of the predator.

The two main assumptions of these equations is that the prey population would grow exponentially if the predator was absent and that the predator consumes the prey with a linear functional response, i.e. the more prey around, the more prey are consumed by the predators.

So what do we want to know about our predator-prey model we just formulated? A good way to start is to see when our populations of predators and of prey are stable, i.e. when dN/dt and dP/dt are equal to zero at the same time, as these are coupled ordinary differential equations.







































Alright, first off, we solve the equations, just like we did for exponential and logistic growth. Note that my formula and the formula used in the graphic are functionally equivalent. The only difference is that we used different letters for the constants.

Next, we plot the solutions of these equations on a phase plane. A phase plane helps one visualize where the rates are equal to zero as well as determining the flow (the growth and number) of the differential equations (populations). When making a phase plane in two dimensions, one normally plots the equilibrium solutions of the differential equations one at a time, then one see on which part of the phase plane would dH/dt (the prey) be bigger or smaller than zero. When dH/dt is greater than zero in a certain region of the phase plane, the flow will be in the positive direction of H (goes to the right). If dH/dt is less than 0 in a certain region of the phase plane, then the flow will go towards negative values of H (goes to the left). On the above diagrams, dH/dt=0 is the horizontal line and dH/dt>0 is below it and dH/dt<0 is above it. For dP/dt (the predator), it is the same principle. On the diagrams, dP/dt=0 is the vertical line, with dP/dt<0 to the left of the isocline and dP/dt>0 to the right of the isocline.

Our stability analysis using isoclines has shown that the predator and prey isoclines are both straight lines and where they will intersect will be the fixed point (a fixed point is a point where the predator and the prey populations do not change over time, i.e. the populations are in stable equilibrium). If one starts with either population away from their fixed point value, then the populations will oscillate around the fixed point forever (this can be seen from the fact that the the trajectories of the flow are closed loops). Therefore, the fixed point is neutrally stable, as the fixed point neither attracts nor repulses the the flow. This also means that the initial conditions of the system determine the length and amplitude of the cycles for an eternity, unless it gets perturbed. If perturbed, it will then go to another neutrally stable cycle. However, in nature, there seems to be populations that show more stable equilibrium dynamics as well as fairly stable cycles that return to those states when perturbed. Therefore, the Lotka-Volterra model of predator-prey dynamics are grossly irrealistic. So how can one improve on the system?

Rosenzweig-MacArthur Model of Predator Prey Dynamics

Well, one way of doing it would be to incorporate more realistic assumptions in the formulations of the equations. Most likely, there would be some density-dependence on the prey, resulting in logistic growth if the predator was absent. In addition, it would be more realistic if the predator could become satiated with prey (i.e. one predator surrounded by one thousand prey items cannot keep consuming at a linear rate, i.e. if there are two prey around, the predator would eat one, if there are 4 prey around, the predator would eat two... if there are 1000 prey around, the predator would eat 500 seems a bit crazy). Rosenzweig and MacArthur created such a model and analyzed its properties:


































Now you might be wondering what Type II means in the equations. Well, it means that we have changed the Type I (linear) functional response for the Hollings Type II functional response (non-linear, asymptotic). I'll go into greater detail about it at a later date as this post is already gigantic. In any event, all one needs to remember is that these changes have great consequences on the dynamics and the stability of the system. First off, their are multiple kinds of stability: We can have a stable fixed point, a neutrally stable fixed point and a unstable fixed point surrounded by a stable limit cycle. These dynamics are fundamentally different from the Lotka-Volterra system. This is mostly do to the shape of the prey isocline and the location of the predator isocline. If the predator isocline is to the right of the maximum (as in the summit of the inverse parabola) of the prey isocline, then there will be a stable fixed point. If the predator isocline is exactly on the maximum of the prey isocline, one would get a neutrally stable fixed point like the Lotka-Volterra system. If, however, the predator isocline is on the left of the maximum of the prey isocline, then the fixed point will be unstable (i.e. repulsive) while a stable limit cycle (the flow goes towards a closed loop) will form around it. If the predator isocline is very far to the left of the maximum, then large oscillations going towards the limit cycle will occur, leading to population levels near zero, hence extinction.

Nevertheless, one may be wondering after all this time spent on these varioius equations and models, what does all this have to do with the Paradox of Enrichment? Well, the link between the Rosenzweig-MacArthur model and the paradox is based upon the carrying capacity, K. As you already know, K is supposed to represent the amount of nutrients in the system available to the prey to grow. Changing the value of K changes the shape of the prey isocline. In fact, what it does, for the most part, is to move the maximum over to the right. Therefore, if one increases K from 3 to 4, as in the diagram above, one can see that the system goes from stable equilibrium to unstable equilibrium. These unstable equilibriums can be more prone to extinction as they undergo oscillations. Therefore, if one increases K, then one also increases the risk of extinctions, reducing the diversity of the system, even though there are more nutrients, hence more individuals could be potentially supported in the area!

So there you have it. The theory behind the original formulation of the Paradox of Enrichment. Of course, this is an extremely simple model and its dynamics are probably irrealistic as well. Nevertheless, there are many natural phenomena that seem to vindicate its main predictions. That will be the next topic explore in this opening series of articles about this blog's namesake.

Note: All figures and diagrams, except for the plain text equations (made by Equation Marker) and the logistic and exponential curves, were taken from lecture 14 of Biology 308: Ecological Dynamics, taught by Gregor Fussman.

Daily Science Quote #10

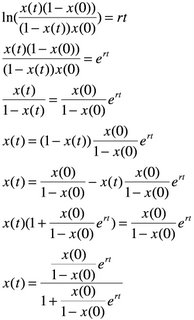
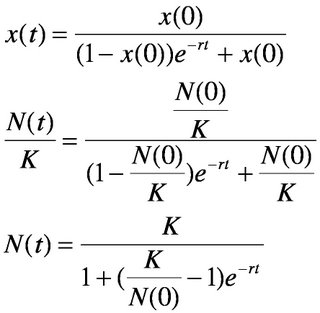
The important thing is not to stop questioning. Curiosity has its own reason for existing. One cannot help but be in awe when he contemplates the mysteries of eternity, of life, of the marvelous structure of reality. It is enough if one tries merely to comprehend a little of this mystery every day. Never lose a holy curiosity.

Albert Einstein

Daily Science Quote #9

Your theory is crazy, but it's not crazy enough to be true.

Niels Bohr

Daily Science Quote #8

Education has failed in a very serious way to convey the most important lesson science can teach: skepticism.

David Suzuki

Daily Science Quote #7

At the same time, science, like other productive activities, like the state, the family, sport, is a social institution completely integrated into and influenced by the structure of all our other social institutions. The problems that science deals with, the ideas that it uses in investigating those problems, even the so-called scientific results that come out of scientific investigation, are all deeply influenced by predispositions that derive from the society in which we live. Scientists do not begin life as scientists after all, but as social beings immersed in a family, a state, a productive structure, and they view nature through a lens that has been molded by their social experience.

Richard Lewontin, in Biology as Ideology, p.3.

Daily Science Quote #6

There is no idea, however ancient and absurd, that is not capable of improving our knowledge. The whole history of thought is absorbed into science and is used for improving every single theory. Nor is political interference rejected. It may be needed to overcome the chauvinism of science that resists alternatives to the status quo.

Paul Feyerabend, in Against Method, p. 5.

Daily Science Quote #5

Nothing in Biology Makes Sense Except in the Light of Evolution.

Title of Theodosius Dobzhansky's 1973 essay on evolutionary biology and creationism.

Daily Science Quote #5

Thus, from the war of nature, from famine and death, the most exalted object which we are capable of conceiving, namely, the production of the higher animals, directly follows. There is grandeur in this view of life, with its several powers, having been originally breathed by the Creator into a few forms or into one; and that, whilst this planet has gone cycling on according to the fixed law of gravity, from so simple a beginning endless froms most beautiful and most wonderful have been, and are being evolved.

Charles Darwin, in The Origins of Species, p.648-649 in my paperback edition.

This is probably the most quoted passage of the book, mostly because Stephen Jay Gould use to quote it in almost all his essays and books. Though usually we omit the first phrase as it is not as pleasing to the mind as the second phrase.

Daily Science Quote #4

All science is either physics or stamp collecting.

Ernest Rutherford, in J. B. Birks Rutherford at Manchester.

As an ecologist, I find physicists' arrogance more amusing than irritating, especially science the majority of physicists I know don't seem to be doing much different science than I am.

Daily Science Quote #3

Scientific claims must be testable; we must, in principal, be able to envision a set of observations that would render them false. Miracles cannot be judged by this criterion, as Whitcomb and Morris have admitted. But is all creationists writing merely about untestable singularities? Are arguments never made in proper scientific form? Creationists do offer some testable statements, and these are amenable to scientific analysis. Why, then, do I continue to claim that creationism isn't science? Simply because these relatively few statements have been tested and conclusively refuted.

Stephen Jay Gould, in Ashley Montagu, ed., Science and Creationism, pp. 130-131.

Daily Science Quote #2

We are survival machines--robot vehicles blindly programmed to preserve the selfish molecules known as genes. This is a truth which still fills me with astonishment.

Richard Dawkins, in The Selfish Gene.